Sarma
Die Methode von Sarma gehört zu dem allgemeinen Lamellenverfahren der Grenzzustände. Sie basiert auf der Erfüllung der Kräfte- und Momentengleichgewichtsbedingungen der einzelnen Blöcke. Die Blöcke entstehen durch das Unterteilen des Erdbereichs über der potentiellen Gleitfläche durch Flächen, welche nach generellen Erfahrungen unterschiedliche Neigungen haben können. Kräfte die auf die einzelnen Blöcke wirken, sind in der folgenden Abbildung dargestellt:
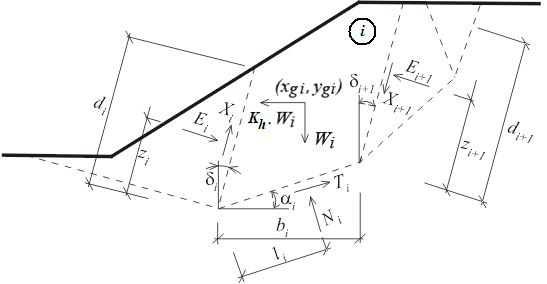Statisches Schema - Methode von Sarma
Hier repräsentieren Ei ,Xi die Normal- und Scherkräfte zwischen den Blöcken. Ni ,Ti sind Normal-und Scherkräfte auf den Abschnitten der Gleitfläche. Wi ist das Blockgewicht und Kh*Wi ist die horizontale Kraft die benutzt wird, um in der Sarma Methode den Grenzzustand zu erreichen. Eine allgemein geneigte Auflast kann auf jeden Block aufgebracht werden. Diese Auflast wird in die Berechnung mit einbezogen, zusammen mit den Ankerkräften und der Auflast, die durch einen freien Wasserspiegel über der Geländeoberfläche entsteht. Alle diese Kräfte werden über die horizontalen und vertikalen Komponenten verteilt, und werden dann in die Kräfte von Fxi und Fyi aufgenommen.
Kh ist die Konstante, der Koeffizient der horizontalen Beschleunigung nennt und wird in die Berechnung eingeführt, um das Gleichgewicht an einzelnen Blöcken zu erfüllen. Es gibt eine Beziehung zwischen Kh und dem Stabilitätsgrad SF für Böschungsbruch, die die Berechnung des Sicherheitsfaktors ermöglicht. Im Normalfall wird mit Kh gleich Null gerechnet. Ein Wert ungleich Null für Kh wird verwendet, um horizontale Belastung zu simulieren, z. B. aufgrund eines Erdbebens (siehe unten).
Berechnungsprozess
Berechnung des Grenzgleichgewichts
In die Berechnung des Grenzgleichgewichts treten insgesamt 6n -1 Unbekannten auf, wobei n die Anzahl der Blöcke ist, auf die wir den Bereich über der Gleitfläche unterteilen. Die Unbekannten sind:
Ei | - | Kräfte zwischen den Blöcken |
Ni | - | Normalkräfte die auf die Gleitfläche wirken |
Ti | - | Scherkräfte die auf die Gleitfläche wirken |
Xi | - | Scherkräfte die zwischen den Blöcken entstehen |
zi | - | Lage der Angriffspunkte der Kräfte |
li | - | Lage der Angriffspunkte der Kräfte |
Kh | - | Koeffizient der horizontalen Beschleunigung |
5n -1 Gleichungen sind für die Unbekannten vorhanden, nämlich:
a) horizontale Kräftegleichgewichtsbedingungen auf Blöcke:
b) vertikale Kräftegleichgewichtsbedingungen auf Blöcke:
c) Momentengleichgewichtsbedingungen auf Blöcke:
wobei rxi und ryi die Hebelarme der Kräfte Fxi und Fyi sind.
d) Beziehungen zwischen Normal-und Scherkräften nach Mohr-Coulomb:
wo: | P*Wi | - | Resultierende Kraft des Porenwasserdrucks auf der Trennfläche |
| - | Durchschnittlicher Wert des inneren Reibungswinkels auf der Trennfläche | |
| - | Durchschnittlicher Wert der Kohäsion auf der Trennfläche |
Es ist ersichtlich, dass n -1 im Voraus gewählt (geschätzt) werden muss. Ein relativ kleine Unkorrektheit wird erziehlt, wenn die Angriffspunkte der Kräfte Ei geschätzt werden. Das Problem ist dann statisch bestimmt. Das Lösen des resultierenden Gleichungssystems liefert dann die Werte der verbleibenden Unbekannten. Das Hauptergebnis dieser Berechnung ist der Koeffizient der horizontalen Beschleunigung Kh.
Berechnung des Sicherheitsfaktors SF
Der Sicherheitsfaktor SF der Böschung wird in die Berechnung eingeführt, um die Bodenparameter c und tgφ zu reduzieren. Die Gleichgewichtsberechnung wird dann für die reduzierten Parameter durchgeführt um den Koeffizient der horizontalen Beschleunigung Kh zu erhalten, der entsprechend dem gegebenen Sicherheitsfaktor SF der Böschung ist. Diese Iteration wird so lange durchgeführt, bis Kh entweder Null ist oder einen eingegebenen Wert hat.
Einfluss der äußeren Belastung
Die analysierte Böschung kann mit einer geneigten trapezförmigen Last beladet werden. Diese Last geht in die Berechnung mit ein, indem die vertikale Komponente (falls sie die selbe Richtung wie die Gewichtskraft hat) zum Gewicht des zugehörigen Blockes dazu addiert wird. Daraus resultiert sowohl eine Änderung des Gewichts der Lamelle, sowie des Schwerpunkts. Falls die vertikale Komponente entgegengesetzt der Schwerkraft wirkt, wird sie zur Kraft Fyi dazu addiert. Die horizontale Komponente wird zu Fxi addiert.
Literatur:
Sarma, S. K.: Stability analysis of embankments and slopes,Géotechnique 23, 423-433, 1973.