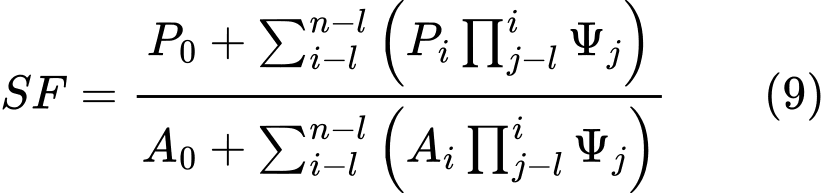Método ITF (Método Fuerza de empuje desequilibrio)
El método ITF es un método del estados límite. Se crea sobre la ecuación de equilibrio de las fuerzas que actúan sobre bloques individuales y no considera la ecuación de momento de equilibrio. Las bases del método y las hipótesis adoptadas son evidentes a partir de la figura siguiente.
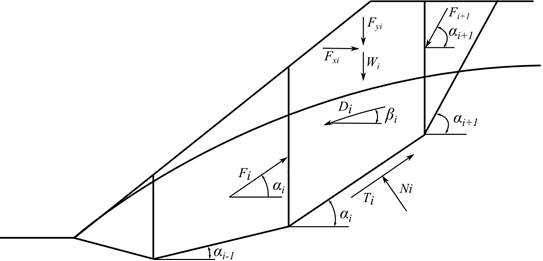 Fig. 1 - Fuerzas actuando en el bloque - Método ITF
Fig. 1 - Fuerzas actuando en el bloque - Método ITF
Tenga en cuenta las siguientes hipótesis en relación a las fuerzas que actúan sobre el bloque:
Donde: | Wi | - | peso del i-ésimo bloque, el peso de una parte del bloque del nivel freático se determina a partir del peso unitario de suelo saturado γSat |
Fyi | - | representa la carga vertical restante que actúa sobre el bloque | |
Fxi | - | representa la carga horizontal restante que actúa sobre el bloque | |
Fi, Fi+1 | - | fuerzas que actúan entre los bloques a lo largo de las direcciones dadas por los ángulos αi y ai + 1 |
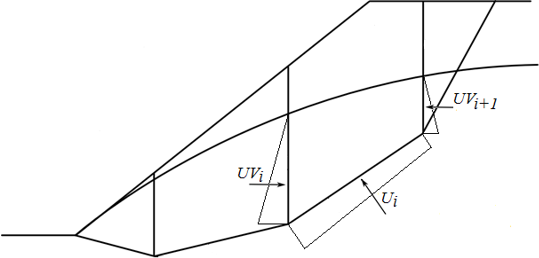 Fig. 2 Esquema de la presión de poros que actúan sobre el bloque
Fig. 2 Esquema de la presión de poros que actúan sobre el bloque
Ui | - | resultante de la presión de poro en el segmento de la superficie de deslizamiento | |
UVi,UVi+1 | - | resultante de la presión de poro en la división de aviones entre bloques |
Las fuerzas UVi y UVi+1 están incluidos en fuerzas horizontales Fxi.
La ecuación de la fuerza de equilibrio en la dirección normal al segmento de la superficie de deslizamiento se proporciona:
![]()
Las fuerzas en el segmento de una superficie de deslizamiento están relacionados por:
![]()
Donde: | φi | - | ángulo de fricción interna del suelo |
ci | - | cohesión de suelo | |
li | - | longitud del segmento de superficie de deslizamiento asociado con el bloque i-ésimo |
La ecuación de la fuerza de equilibrio en la dirección de la i-ésimo segmento de la superficie de deslizamiento (dada por el ángulo αi) produce la fuerza Fi que actúa entre los bloques en la forma:
![]()
Presentación de las Ecs. (1) y (2) dentro de la ecuación. (3), establece:
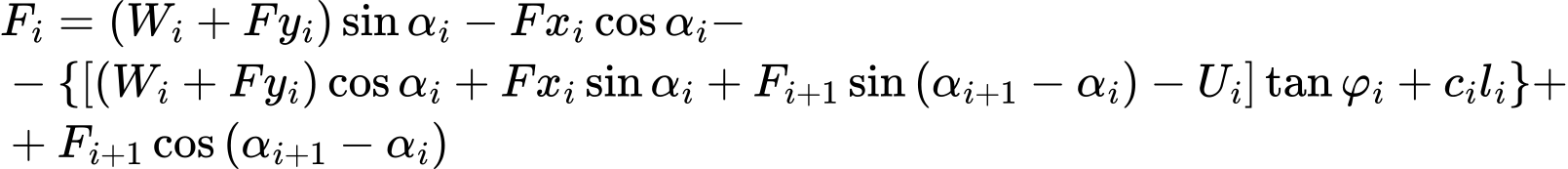
y después de algo de álgebra formal, se llega a la forma resultante de la ecuación de equilibrio:
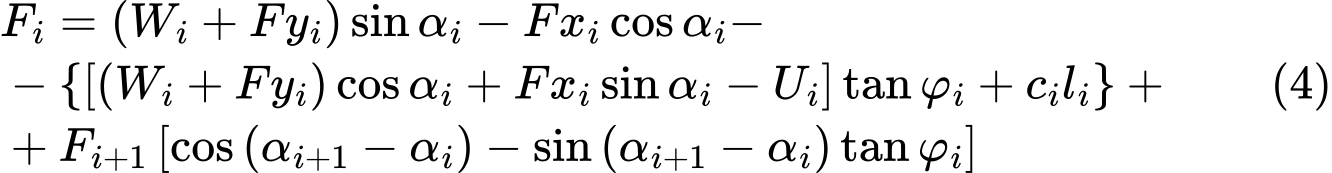
La condición de equilibrio se cumplirá mediante la introducción del factor de seguridad SF en el análisis, de tal manera que los parámetros de resistencia de un suelo dado c y tanφ se dividan por este valor. Ecuación. (4) a continuación, se convierte en:
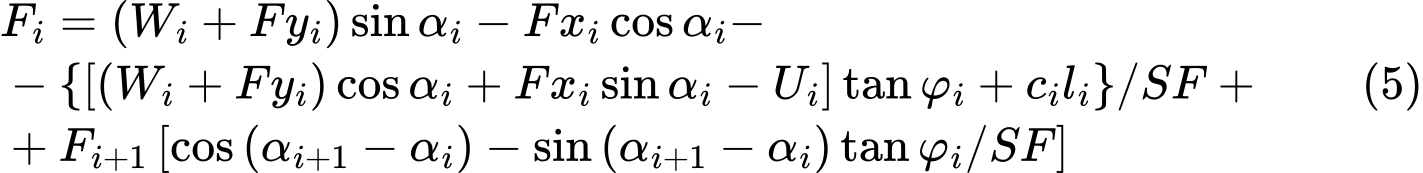
La ecuación. (5) a continuación, da el factor de seguridad buscado de SF a través del proceso de iteración. Este proceso continúa tal que la fuerza Fn igual a 0 kN se aplica en el punto más alto (final) de la superficie de deslizamiento. Las fuerzas Fi actuando en entre bloques se determinan para un valor dado del factor de seguridad SF de la ecuación (5). Este paso se repite para varios valores de SF hasta que encontremos tal SF para lo cual la fuerza F0 en la base de la pendiente se hace igual a 0 kN. No se asume la tensión a lo largo de la superficie de deslizamiento. La condición de equilibrio requiere que el valor de la fuerza normal Ni sea negativo, lo que significa que el suelo se carga en tensión, entonces el valor de esta fuerza se fija igual a cero en la siguiente etapa de iteración y la fuerza de corte Ti que actúa sobre un segmento dado se determina en base a la cohesión del suelo.
El método ITF es muy sensible con respecto a la forma de la superficie de deslizamiento. En caso de que la superficie de deslizamiento contiene segmentos discontinuos agudos el factor de seguridad resultante es generalmente más grandes como comparar a la realidad. Se recomienda que la diferencia de pendiente entre segmentos adyacentes de la superficie de deslizamiento sea menos de 10°. Esto se comprueba de forma automática por el programa y si la diferencia de pendiente encontrada es mayor a lo sugerido por el programa, le mostrará una advertencia de que los resultados podrían estar sobreestimados. Esto por lo general no es el problema de una superficie de deslizamiento circular, pero debe tenerse en cuenta en el caso de superficies de deslizamiento poligonales.
Método ITF - solución explícita
La solución explícita del método ITF asume una forma diferente de introducción del factor de seguridad en el análisis. La solución matemática a continuación, no requiere de iteraciones y el factor de seguridad resultante se calcula directamente en un solo paso. Con este enfoque, el factor de seguridad resultante es típicamente más alto, lo que puede dar una solución totalmente devalada, en particular en los casos relativos a superficies de deslizamiento poligonales con grandes diferencias de pendiente de los segmentos adyacentes.
La solución de la ecuación (4) se expone como el factor de seguridad SF que se introduce de tal manera que multiplica los componentes activos de las fuerzas, es decir, los componentes que actúan en la dirección de deslizamiento. La condición de equilibrio se convierte entonces en:
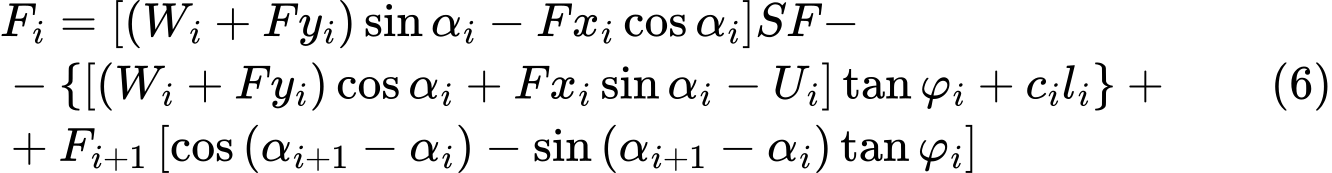
Para lucidez introducimos el componente de fuerzas activas como:
![]()
y luego los componente de fuerzas pasivas como:
![]()
y una función auxiliar:
![]()
La ecuación (6) puede ser escrita a continuación, en forma más compacta como:
![]()
El siguiente paso supone la fuerza conocida Fn = 0 para proporcionar expresiones de fuerzas entre los bloques F en la forma:
![]()
![]()
![]()
Etc….
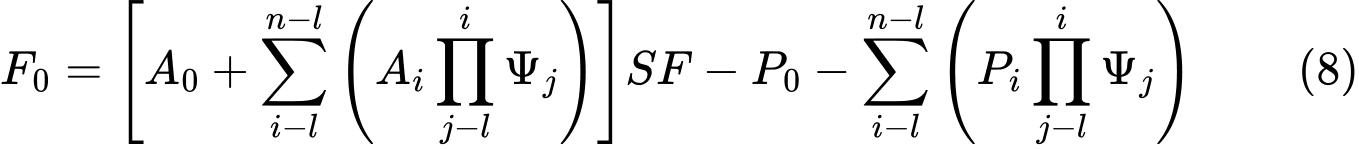
Y como la fuerza en la parte inferior origen de la superficie de deslizamiento debe ser igual a 0 kN, se obtiene la forma final del factor de seguridad SF como: