Teoría de asentamiento primario
El asentamiento primario final s es normalmente substituido por el término asentamiento. La mayoría de los métodos de cálculos pueden estar conectados a unos de estos dos grupos:
- Deformación elástica lineal
- Deformación elástica no lineal
Deformación elástica lineal
La relación tensión-deformación lineal sigue la ley de Hook:
![]()
Donde: | ε | - | Deformación inducida por la tensión efectiva en la capa del suelo |
Δσef | - | Cambio inducido por la tensión efectiva en la capa del suelo | |
E | - | Módulo Young en la capa del suelo | |
ν | - | Coeficiente de Poisson |
La aplicación del módulo de Young de elasticidad E es justificada solo en el caso, en el que se permite a la tensión del suelo estirarse en dirección horizontal. Esto, sin embargo, se permite solo para pequeñas extensiones de cimentación. Cuando se aplica la carga sobre un área mayor, el suelo tensionado no puede, excepto en sus extremos, deformar sus lados; y experimenta solo una deformación vertical (en una sola dirección) relacionada con el módulo edométrico Eoed, que es mayor al módulo elástico E.
El asentamiento de la capa de suelo s, se determina multiplicando la deformación de la capa de suelo ε por el espesor de la capa (altura) Ho:
![]()
Donde: | ε | - | Deformación de la capa del suelo |
Ho | - | Espesor de la capa del suelo |
En el caso de subsuelos en capas, se obtiene el asentamiento total sumando el asentamiento de cada capa individual:
![]()
Donde: | s | - | Asiento en las capas del subsuelo |
εi | - | Deformación de la capa del suelo ith | |
Hoi | - | Espesor de la capa del suelo ith |
Deformación elástica no lineal
Para la mayoría de los suelos, la relación tensión-deformación es no lineal y es normalmente influenciada por la carga histórica. Esta no-linealidad no puede ser ignorada, particularmente cuando se calcula el asentamiento para suelos de grano fino (limo, arcilla). Claramente, el proceso basado en la aplicación del módulo de elasticidad de Young, no es generalmente aplicable. Incluso empleando la tensión dependiente del módulo edométrico de deformación, no será posible obtener estimaciones razonables del comportamiento de ciertos suelos sobre-consolidados.
La deformación elástica no lineal es generalmente modelada utilizando el índice de vacío y las características de deformación son derivadas de la deformación unidimensional de una muestra de suelo. (ej.: constante de compresión, índice de compresión, etc.).
El procedimiento para calcular el asentamiento de una capa de suelo compresible saturado utilizando el índice de vacío e, se describe en el siguiente elemento de suelo con una altura de Ho y un ancho de B = 1 m:
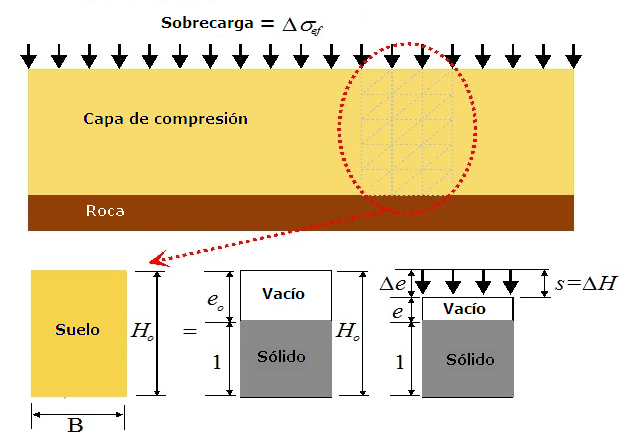 Análisis de asiento del diagrama de fase
Análisis de asiento del diagrama de fase
Debido al hecho de que el suelo es un medio de tres fases (contiene partículas sólidas y poros llenados con fluidos y gas) es posible describir las partículas sólidas (partículas de rocas y granos minerales) por sus volúmenes Vs (y se asume igual a la unidad) mientras que la fase porosa puede ser descripta utilizando el índice de vacío e.
El elemento suelo es sometido, en su superficie superior, a un carga uniforme q, que causa cambios en la tensión dentro de la muestra e incluso un desplazamiento vertical ΔH, el cual a su vez conduce a la reducción de poros Vp y así también a la reducción del índice de vacío (del valor original eo hacia un nuevo valor e). La deformación vertical ε de la muestra del suelo está dada por el índice de ΔH a la altura de la muestra original Ho, y puede ser expresada utilizando el índice de vacío e:
![]()
Donde: | ε | - | Compresión relativa vertical |
ΔH | - | Deformación vertical | |
Ho | - | Altura original del elemento | |
s | - | Asiento | |
e | - | Índice de vacío | |
Δe | - | Cambio en el índice de vacío |
Modificando esta ecuación se llega a la fórmula que describe la muestra de asentamiento con la ayuda del índice de vacío:
![]()
Donde: | ε | - | Compresión relativa vertical |
Ho | - | Altura original del elemento | |
s | - | Asiento | |
e | - | Índice de vacío | |
Δe | - | Cambio en el índice de vacío |