Hướng dẫn trực tuyến

Assentamento Primário

O assentamento primário final s é muitas vezes substituído pelo termo assentamento. A maioria dos métodos computacionais pode ser englobada em um destes dois grupos:

• Deformação elástica linear
• Deformação elástica não linear

Deformação elástica linear

A relação tensão-deformação é dada pela lei de Hook:

A aplicabilidade do módulo de Young E da elasticidade é fundamentada apenas em casos em que o solo tensionado pode expandir-se na direção horizontal. No entanto, apenas é aceitável para pequenas fundações contínuas. Ao aplicar a carga sobre um área maior, o solo tensionado não se deforma lateralmente, exceto nas extremidades, e experimenta apenas uma deformação vertical (unidimensional) relacionada com o módulo edométrico E_oed, que é superior ao módulo E.

O assentamento de uma camada do solo s é determinada a partir da deformação da camada do solo ε pela espessura da camada (altura) H_o:

No caso de subsolos em camadas, o assentamento total é obtido a partir do somatório dos assentamentos de cada camada:

Deformação elástica não linear

Para a maioria dos solos, a relação tensão-deformação é não linear e muitas vezes influenciada pelo histórico do carregamento. Esta não linearidade não pode ser desprezada, particularmente ao computar o assentamento de solos de graduação fina (siltes, argilas). O procedimento baseado na aplicação do módulo de Young da elasticidade não é, geralmente, aplicável. Mesmo ao aplicar a tensão dependente do módulo edométrico de deformação, não será possível obter estimativas razoáveis do comportamento de certos solos sobreconsolidados. A deformação elástica não linear é modelada através do índice de vazios e as características da deformação são derivadas da deformação unidimensional de uma amostra de solo (ex.: constante de compressão, índice de compressão, etc.).

O procedimento para a computação do assentamento de um solo saturado compressível através do índice de vazios e é demonstrado a partir do elemento de solo seguinte, com altura H_o e largura B = 1 m:

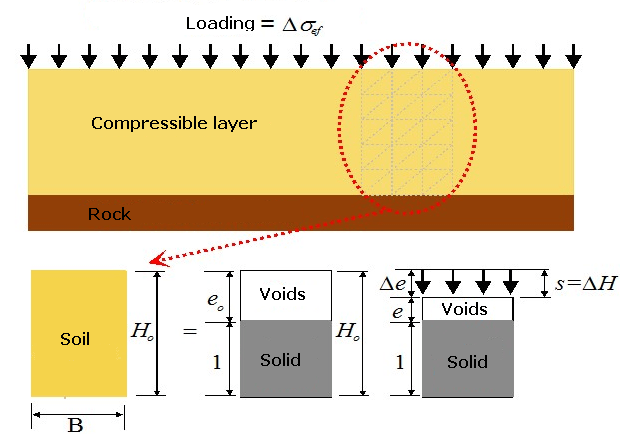Análise de assentamento a partir de diagrapa de fase

Devido ao facto de que o solo é um meio trifásico (contém partículas sólidas e poros preenchidos com fluídos e gases), é possível descrever as partículas do solo (partículas de rochas e grãos minerais) pelo seu volume V_s (e assumi-lo como igual a um), enquanto que a fase porosa pode ser descrita pelo índice de vazios e.

O elemento do solo está sujeito, na sua superfície superior, a uma carga uniforme q, que causa uma variação de tensão no interior da amostra e no deslocamento vertical ΔH, que leva a uma redução dos poros V_p e, consequentemente, à redução do índice de vazios (desde o seu valor original e_o até ao seu novo valor e). A deformação vertical ε de uma amostra de solo é dada pelo rácio de ΔH até à sua altura original H_o e pode ser exprimida através do índice de vazios e:

Ao modificar esta equação, é possível obter a fórmula que descreve o assentamento da amostra através do índice de vazios: